宜兴外国语学校 裴姣
摘要:数学概念教学是双基教学的核心,是数学能力培养的基础。抽象思维贯穿概念生成的全过程,概念课教学应经历生活实例引入、抽象概括形成、反例对比巩固、回归生活落实四个环节,概念的生成过程是抽象思维的落实与提升过程。
关键词:抽象思维;核心素养 ;概念;探究
“双减”背景下,高效的课堂是我们要努力追求的,在新课教学中,抓住双基教学的核心,让学生充分理解和掌握数学概念,才能实现教学的高效性。课程标准指出:在教学中引导学生经历从具体实例抽象出数学概念的过程,在初步应用中逐步理解概念的本质。教学中概念的生成过程,就是数学的抽象过程。下面,笔者以苏科版八年级上册第六章第2节“一次函数”(第1课时)的教学为例,阐述如何落实概念的过程教学,培养数学抽象思维,提升数学核心素养。
一.课例呈现
环节1.创设情境,引入概念
问题情境:我国国庆阅兵的方队人数是世界上最多的。其中徒步方队的编成队形,大部分为25×14+2,也就是正面25人,纵深14排,领队2人,一个方队总人数是352人。
(1) 方队中从前往后数至x排时,总人数y(人) 与排数x(排)之间有什么关系?
(2)为了保证动作整齐划一,队伍保持每分钟行进112步,队伍行进总步数w (步)与行进时间t(分) 之间有什么关系?
问题:能解决这两个问题吗?带着问题一起回顾阅兵式精彩片段。
设计意图:通过观看视频,学生再次感受国庆阅兵气势磅礴的壮观场面,产生深深的民族自豪感的同时,发现等量关系:方队总人数=每排人数 排数+领队人数,行进总步数=每分钟行进步数
排数+领队人数,行进总步数=每分钟行进步数 行进时间。通过探索简单实例中的数量关系和变化规律,回顾变量、常量概念,为探究一次函数概念做好知识储备。
行进时间。通过探索简单实例中的数量关系和变化规律,回顾变量、常量概念,为探究一次函数概念做好知识储备。
增设实例,加强感知
问题1:给汽车加油的加油枪流量为22L/min,如果加油前油箱里没有油,那么在加油过程中,我能知道油箱中的油量吗?(1)油箱里的油量y(L)与加油时间x(min)之间有怎样的函数表达式?(2)如果加油前油箱里有6L油呢,油量y(L)与加油时间x(min)之间有怎样的函数表达式?
问题2:小张家离校约3000米,小张以每分钟行驶300米的速度骑自行车上学,小张早上上学从家出发骑行x分钟时,离开学校的路程y(米)与骑车时间x(分)之间有怎样的函数表达式?
问题3:某弹簧的自然长度为3厘米,在弹性限度内,所挂物体的质量x每增加1千克,弹簧长度y增加0.5厘米。在弹性限度内,弹簧长度y与所挂物体的质量x之间有怎样的函数表达式?
问题:(学生解决3个问题后)想一想,这些函数表达式来源于哪里?(生活中)函数表达式来源于生活,我们研究就是从生活中的问题到函数问题。
设计意图:数学来源于生活,通过探究大量的生活实例,用数学语言予以表示得到描述一般规律和结构的数量关系,抽象出函数表达式,进一步发展了学生的抽象思维。章建跃博士指出,提升概念教学水平,最根本的是抓住数学概念的过程教学,选取学生熟知的典型生活实例,并提供丰富素材,让学生经历完整的数学抽象过程。
环节2. 探究特征,归纳概念
探究活动一:观察这些函数表达式,有什么共同特征?
(1)y=25x+2 (2)w=112t (3)y=22x
(4)y=22x+6 (5)y=3000─300x (6)y=0.5x+3
问题:这一类函数有什么特别之处?我们一起观察表达式,说出共同的特征。(讨论)
设计意图:引导学生将列举的函数充分观察,寻找共性,大胆归纳,各抒己见,逐步得出:它们都是关于自变量的一次整式。老师适时小结,这类函数的自变量次数都是1,这类特殊的函数叫一次函数,既点明课题,也解释了它是按自变量的次数进行分类命名的,为后续学习二次函数打好基础。
概念:形如y=kx+b(k ,b为常数,k≠0 )的函数叫做一次函数,其中x是自变量,y是x的函数。
探究活动二:
问题:说出以上一次函数中的k与b.
追问1:你能对以上一次函数进行分类吗?为什么这样分?
追问2:正比例函数是一次函数吗?
设计意图:运用归纳出的一次函数表达式的一般形式,让学生从不同形式的表达式中找出常量k与b,本质上是确定一次函数表达式中自变量的系数与常数项,进一步加强学生对一般形式的结构特征的理解,强化学生对概念的认知。追问如何分类,又不给出分类的标准,倡导学生大胆思考独立处理问题,具有开放性。学生充分回答后,再探讨式子(2)(3)和(1)(4)(5)(6)有什么共同和不同之处,让学生感受正比例函数是一次函数的特例。
概念:特别地,当b=0时, y=kx(k为常数,k≠0)y叫做x的正比例函数。
环节3.概念辨别,练习巩固
问题1:判断下列表达式是一次函数吗?是正比例函数吗?
① y=x-6 ② y= 2x2+3 ③ y=  ④ y=
④ y=  ⑤ y= 5 ⑥ y= kx(k是常数)
⑤ y= 5 ⑥ y= kx(k是常数)
所以,y是x的一次函数的有( );y是x的正比例函数的有( )。
设计意图:通过观察不同形式的表达式,自我回顾变量、常量的概念,审查自变量的次数是否为1做出判断与筛选,这样对比呈现的题型形式更容易清晰学生的知识脉络,形成系统知识结构。需特别注意的是最后一个表达式要对常数k进行条件限制,若无k≠0的条件,该函数不是一次函数。
问题2:例题(1)当m取何值时,函数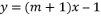 是一次函数?
是一次函数?
(2)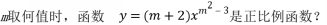
设计意图:分析题目条件,自变量的次数是确定值1,仍需给学生充分时间思考,根据函数概念只有两个变量,式子中的字母系数是满足特定条件的常量,进一步得出自变量的系数满足不能是零的限制条件。
问题3:体会表达:用自己的语言来介绍一下一次函数。
设计意图:抽象的函数要用语言描述出来,学生需对函数概念和一次函数特征有较深刻的了解体会,鼓励学生用自己的语言去描述,培养学生语言表达能力和相互合作意识。学生描述中是否加入正比例函数,检测他们是否真正理解正比例函数与一次函数间的关系,引发他们的再次思考,深化概念。
环节4.源于生活,回到生活
问题1:用函数表达式表示下列变化过程中两个变量之间的关系,并指出其中的一次函数、正比例函数。
(1)正方形面积s随边长x变化而变化;
(2)正方形周长l随边长x变化而变化;
(3)长方形的长为常量a时,面积S随宽x变化而变化;
(4)高速列车以300km/h的速度驶离A站,列车行驶的路程y(km)随时间t (h)变化而变化;
(5)如图,A、B两站相距200km,一列火车从B站出发以120km/h的速度驶向C站,火车离A站的路程y(km)随行驶时间t(h)变化而变化.

设计意图:引导学生结合具体情境体会一次函数和正比例函数的意义,再次感受正比例函数是一次函数的特例。让学生不但学会知识,更学会应用知识,让数学知识回归生活,体现数学源于生活又服务于生活的理念。
问题2:请你用熟悉的生活情景,设计一个用正比例函数表示的实际情境和一个用一次函数表示的实际情境。
设计意图:学生可先设计函数表达式,然后赋予不同的生活背景。若两个函数编在同一问题情境,只通过变化个别条件予以区分,编题效果更佳。通过编题,不仅发散了学生的思维,又再次体现运用数学知识服务于生活的理念。
环节5.理解概括,深化提升
问题:请你概括一下,( )的一次函数。
设计意图:学生可以从知识特征、探索过程、思想方法、情感体验等不同的角度进行回顾总结,开放性的问题更易启发学生思考,反思知识的探究过程,形成自我情感体感,提升自我的数学核心素养。
二.反思
1.在大量生活实例中引入概念
概念教学既不能灌输概念,也不能让学生死记硬背,应创设贴近学生实际的生活情景,让他们产生探究的兴趣,思考的积极性也会提高。本课以生活中的原型为素材,除了阅兵式问题,还增设了加油枪、离学校距离、弹簧长度3个问题,意在让学生通过大量生活实例,抽象出函数表达式,这样由具体到抽象的思维过程,符合学生的认知规律和抽象思维的特点。
2.在抽象概括中形成概念
本课探究活动一寻求6个函数表达式的共性,探究活动二对6个函数表达式进行分类。两个探究活动过程,是抽象思维的生长点,实现表象到本质,具体到抽象的思维特点。形成概念经历分析问题—列出式子—观察猜想—提取共性—总结规律—表征概念着一系列的过程,让学生体验和感悟了一次函数产生的过程,也为后续得出二次函数的概念指明方向。
3.在与反例的对比中巩固概念
数学概念的巩固不一定要在特征属性这条道一走到底,另辟蹊径,反其道而行之亦能收到良好的效果,其中反例教学就是不错的方法。本课环节3问题1辨析概念中,加入自变量不是1,缺少1个变量等一些反例,让学生辨析,对比后更能突显一次函数和正比例函数的特征,清晰概念本质,巩固概念。
4.在回归生活中落实概念
研究问题的目的是为了解决问题。本课从生活问题抽象出数学问题,最终又用数学知识来重新认识生活中的问题。环节3问题4中用函数概念来解释生活中处处存在的生活实例,体现数学来源于生活又服务于生活的本质。用数学的眼光观察世界,用数学的语言表达世界,回归生活是数学抽象思维的归宿。